COMPUTATIONAL PHYSICS & BIOLOGY
At NANOTEC, a well-structured theoretical-computational research activity develops in collaboration with experimental research.
CONTACT PERSONS
Alessandra S. Lanotte, Stefania D’Agostino, Luca Leuzzi,
Giuseppe Palma, Giuseppe Pucci, Bruno Rizzuti, Eugenio Vocaturo
KEYWORDS
Glassy & Disordered Systems, Molecular Dynamics, Complex Flows & Fluid Dynamics, HPC, Light-Matter Interaction, Quantitative and Statistical Image Processing
It focuses on:
- systems with many interacting constituents, from glasses and spin glasses to soft and biological matter
- the physics of complex flows and complex fluids;
- the analysis of biological systems, from single-molecules to biological networks and system-level properties;
- the analysis of processes of light-matter interaction of interest for molecular plasmonics, polariton chemistry and topology;
- theoretical approaches to quantitative Magnetic Resonance Imaging and statistical modeling of radiotherapy outcomes
In addition, we are interested in the development of efficient algorithms for inference and big data analysis to be run on HPC facilities, from Leonardo Supercomputer to DARIAH Data Center, the new-generation cluster hosted by CNR-NANOTEC.
Research lines are detailed here below:
Statistical Mechanics of Complex Disordered Systems
In recent years, random lasing materials (e.g. powders, porous media, precipitates in solution, or photonic crystals with impurities) have been extensively studied experimentally.
Contact Persons
Luca Leuzzi
Keywords
multi-equiibria complex systems, spin-glass, glassy systems, critical slowing down, off-equilibrium statistical mechanics, machine learning, phase retrieval, photonics in random media, optical computing.
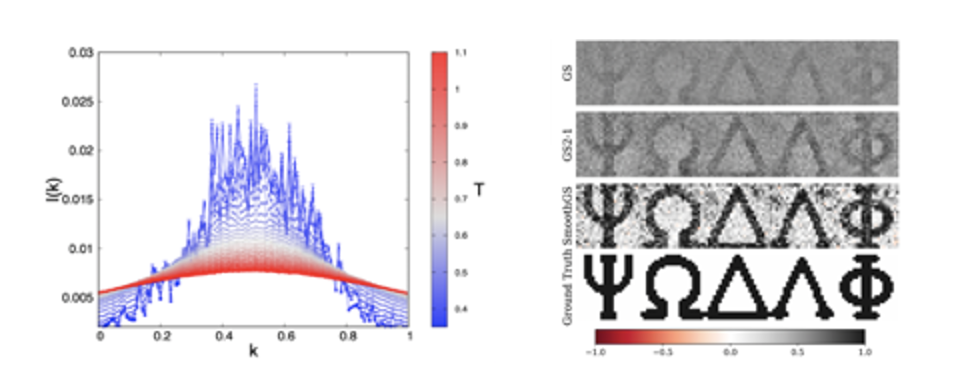
Pumping energy into these systems causes them to re-emit multi-mode coherent light, with a spectrum displaying randomly arranged peaks in frequency. Starting from the structure and geometry of the atoms and molecules that scatter the light waves, one would like to formulate a theory that predicts the onset, the nature and the features of the light modes, and answering relevant questions, such as: what shape and size do light modes display in space? In which dimension and under which conditions do they localize because of disorder? At which frequencies do light modes emit in cavity-less media? Can there be a random laser pulse in time?
Glassy Random Laser and Experimental Measurement of Replica Symmetry Breaking. The investigation of the glassy behaviour of light in the framework of our theory is made possible by means of a newly introduced overlap parameter, the Intensity Fluctuation Overlap (IFO) measuring the correlation between intensity fluctuations of waves in random media. This order parameter allows to identify the laser transition in arbitrary physical regimes, with varying amount of disorder and non-linearity. In random media, it allows for the identification of the glassy nature of some kind of random laser, in terms of emission spectra data, the only data so far accessible in random laser measurements. A generalised complex spherical spin-glass model solvable in the mean-field approximation by Replica Symmetry Breaking (RSB) theory of G. Parisi can be applied. IFO measurements are possible in real experiments, recently leading to a validation of the RSB theory and a characterisation of lasers in terms of spectral intensity fluctuations.
Glassy and slowly relaxing systems. A glass can be viewed as a liquid in which a huge slowing down of the diffusive motion of the particles has destroyed its ability to flow on experimental timescales. Starting from the liquid phase and by supercooling the system, the viscosity of the melt grows several orders of magnitude in a relatively small temperature interval (i.e. the mobility of the atoms or molecules decreases by many orders of magnitude). This loss of mobility makes it impossible to reach thermodynamic equilibrium: the system is said to have fallen out of equilibrium. We work on the theoretical representation of the behavior of viscous liquids, structural glasses and spin-glasses, on the critical slowing down occurring near-by the dynamic arrest, on the aging dynamics, on the extension of glass theories beyond the limit of validity of mean-field approximation.
Inverse problems in statistical mechanics, statistical inference and phase retrieval. Given a data set and a model with some unknown parameters, the inverse problem aims to find the values of the model parameters that best fit the data. We focus on systems of interacting elements, in which the inverse problem concerns the statistical inference of the underling interaction network and of its coupling coefficients from observed data on the dynamics of the system. Versions of this problem are encountered in physics, biology, social sciences and finance, neuroscience (just to cite a few), and are becoming more and more important due to the increase in the amount of data available from these fields. We work on the analysis of the performances of the various inference methods, on their improvement and on their application to new problems.
Analogic computing, classification tasks. In the domain of disordered photonics, the characterization of optically opaque materials for light manipulation and imaging is a primary aim. Among various complex devices, multi-mode optical fibers stand out as cost-effective and easy-to-handle tools, making them attractive for several tasks. In this context, we represent these fibers as models projected into random hardware projectors, transforming an input dataset into a higher dimensional speckled image set. We also work on the implementation of physical neural networks made of polaritonic substrates in classification problems and reservoir computing, theoretically studying the effective interaction among condensates on a lattice and numerically assessing the performances of thus-built systems as neural networks in classification and computing problems.
People
Luca Leuzzi, Federico Ricci Tersenghi, Enzo Marinari, Ilaria Paga, Stefano Bae, Marcello Benedetti, Luca Maria Del Bono, Giacomo Trinca-Cintioli
Computational Biology
Theoretical methods and mathematical modelling can be used to investigate complex biological systems. Computer simulations are particularly important for studying in atomic detail the interactions of biological macromolecules, especially proteins.
Contact Persons
Bruno Rizzuti
Keywords
molecular dynamics, protein folding, drug design, binding interactions
We are interested in developing accurate computational protocols for modelling several challenging molecular targets, including multimeric assemblies and intrinsically disordered proteins, especially in interaction with small bioactive compounds. Applications are envisaged in the identification of the molecular basis of diseases, and in several nanomedicine applications such as the computer-aided rational design of drugs.
Disordered protein states. The ordered structure of proteins is one of the fundamental paradigms of classical biology and explains many aspects of their function. Nevertheless, in many cases proteins operate in environments that are far from equilibrium or possess labile conformations that convert to order only under specific conditions. Examples include protein folding/unfolding in the presence of temperature and pressure variations, or configuration reorganizations induced by the binding to molecular partners in intrinsically disordered proteins. The statistical properties of these ensembles of structures can be studied using sampling techniques based on classical molecular dynamics simulations.
Protein-protein interactions. Interactions between and among proteins play a key role in biological networks and dictate their structural evolution in the long run. Modeling these phenomena in atomic detail by using computer simulations is particularly difficult, because their spatial and temporal scale can be extremely large. For instance, both transient and permanent complexes can be formed, sometimes depending on subtle changes in temperature, pH, and other conditions in the biological environment. Computer simulations can be used to predict the structure of supramolecular assemblies, and the binding free energies of the reactions that determine the formation of such complexes.
Ligand binding. Interactions between macromolecules and ligands are responsible for molecular recognition, binding, transport and release of molecules that are important from a functional point of view. These mechanisms are fundamental in many processes that are vital for any living organism and can be exploited in several nanotechnology applications. We use molecular dynamics simulations and docking calculations to determine a model of interaction between a variety of ligands and macromolecules belonging to different species, including proteins and lipid membranes. We can predict structural and dynamical properties of the functionality of a molecular complex, for instance between transport proteins or cell receptors with small inorganic compounds that include molecules of physiological and pharmacological interest.
People
Bruno Rizzuti, Rita Guzzi
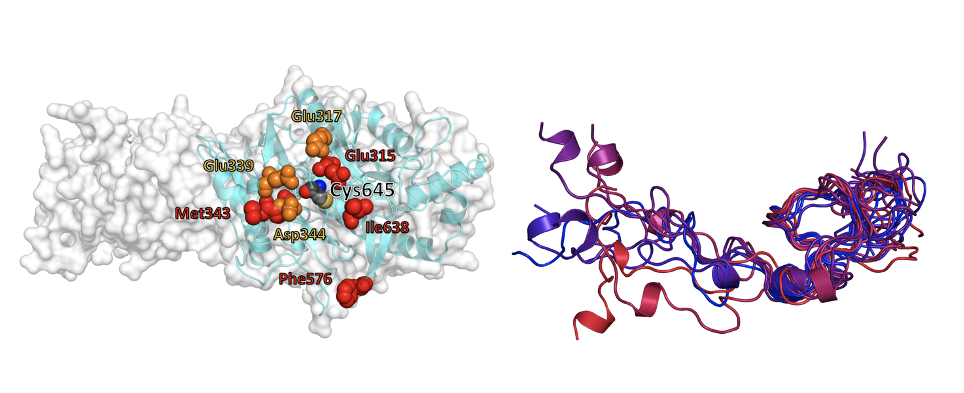
Figure: Computational modeling of challenging protein targets. (Left) Binding patch around the catalytic site in the monomer of a multimeric protein. (Right) Structural ensemble of an intrinsically disordered protein in solution.
Fluid dynamics for complex flows & complex fluids
Our research addresses the dynamics of fluid systems that are complex because of the simultaneous presence of particles; or because they are at cryogenic temperatures, and classical and quantum effects are at play; or because they are in a complex statistical state, such as turbulent ones.
Contact Persons
Alessandra S. Lanotte, Giuseppe Pucci
Keywords
turbulent suspensions, quantum fluid dynamics, fluid interfaces, wave-driven particles, hydrodynamic quantum analogs, wave-mediated active systems
Turbulent-like systems. Turbulence is not a single problem, but rather a huge field of interdisciplinary research with applications to different disciplines: we are interested in fundamental questions, motivated also by applications, linked to the statistical properties of the carrying fluid itself and to the advection/diffusion of particles and fields transported by the flow.
Applications: complex flows in industry and environment, dynamics of colloidal aggregates, evolution and transport of sediments or suspended matter in natural fluids; fluid dynamics of quantum systems.
In complex fluids, i.e., mixtures in which two or more phases coexist. We are interested in rotating stratified flows, fragmentation dynamics of aggregates in turbulent and laminar flows, transitions from (D) to (D-1) dimensional dynamics.
Quantum fluid dynamics. Classical and quantum physics arise in the study of two-dimensional exciton-polariton quantum fluids. Loosely speaking, these are super fluids – fluids with zero viscosity- emerging from the strong light-matter interaction in semiconductor microcavities. In many applications, a mean field theoretical approach can be used, resulting in an effective non-linear Schrödinger (NLS) equation for the wave function of the condensate. We work in close collaboration with the experimental investigation of quantum fluids of light at NANOTEC (Advanced Photonics group).
Numerical tools – developed in house- are supported by a professional knowledge about the optimization of software for massive parallel machines hosted in the European supercomputing centers. We are engaged in the national High-Performace Computing community, with national grant allocations at CINECA, and have many times benefited of EU allocations within the PRACE framework.
Wave-like phenomena. We also investigate the wave-mediated interactions at liquid/air interfaces both experimentally and theoretically to develop hydrodynamic quantum analogs and wave-mediated active systems.
Hydrodynamic quantum analogs. In the last two decades, several quantum-like behaviors have emerged in macroscopic fluid systems in which a particle is coupled to a wave. We are interested in broadening and refining the analogy between these classical systems and their quantum counterparts, motivated by the following question: to what extent can a classical wave-driven system reproduce behaviors usually thought to be peculiar to the quantum realm? This question is addressed with fluid dynamics experiments, modeling, and theoretical models inspired by fluid systems.
Wave-mediated active systems. Active systems are composed of particles that use internal or environmental energy to move or interact. We are interested in the dynamics of particles driven by and interacting with waves at a liquid/air interface. We focus on phenomena occurring at the capillary scale, at which surface tension is relevant, and study collective behaviors.
People
Alessandra S. Lanotte, Giuseppe Pucci, Riccardo C. Barberi, Wilson Reino

Figure: Capillary surfers, in the figure above, are wave-driven particles that self-propel and interact on a fluid interface via an extended field of surface waves.
Light-matter interaction
The response of materials to electromagnetic stimulation depends on both the atomistic structure of matter and its environment. This is an incredibly captivating subject that draws interest from various scientific communities, ranging from quantum chemistry to nanophotonic.
Contact Persons
Stefania D’Agostino
Keywords
plasmonics, molecular plasmonics, polariton chemistry and topological materials
The Light-Matter Interaction group aims at investigating in the quantum-mechanical framework of Density Functional Theory (DFT), the structural, electronical and optical properties of systems going from finite atomistic objects of interest for quantum chemistry (e.g. molecules or nanoclusters), to 3D or 2D periodic materials pertaining to condensed matter physics and presenting exotic properties (i.e. topological insulators). The group activity can be summarized as follows.
Polariton Chemistry. On demand control of photochemical processes can be achieved by strongly coupling between optical excitations of molecules and photonic modes. In this regime of interaction, the photonic and molecular states hybridize into new half-light/half-matter states, named polaritons. Several experimental and theoretical studies have shown how polaritonic modes induced perturbations on the quantum yield and kinetics of several chemical reactions, given origin to Polariton Chemistry. The idea of the group is that to study, by calculating the polariton PESs (Potential Energy Surfaces), how to achieve an on-demand control of the photochemistry of some photo switches, such as azobenzene, via Localized Surface Plasmons (LSPs), sustained by noble-metal nanoclusters.
Adiabatic and Non-adiabatic Molecular Dynamics. To control the direct and indirect effects of metal nanoparticles on the photochemistry of photo switches in realistic biological environments, Molecular Dynamics (MD) analysis is required. These can be classical MD simulations to follow diffusion processes including millions of atoms and to set up the region of interest to be studied in quantum mechanics/molecular mechanics (QM/MM) approaches or quantum MD simulations to follow the effects of plasmons on the non-adiabatic dynamics of the photo-reactive centers. Currently the group is studying the interaction of an Au cluster with Channelrhodopsin (ChR), a protein which features a retinal chromophore that, upon light absorption, undergoes a photoisomerization activating the photocycle, a cascade of events that drives the protein to the ion conducting state. This, in turn, leads to depolarization of the cell membrane in which the protein is inserted and can be used to trigger the activity of neuronal cells. The ChR photosystem, thus, enables scientists, by using light to manipulate neuronal activity, to selectively activate or inhibit specific neurons in living organisms, including animals and even in some cases, in human tissue cultures (i.e. optogenetics).
Topological Materials. Topological insulators are a fascinating class of materials that exhibit unique electronic properties due to their topological nature. Unlike conventional insulators, which present an energy gap between a filled valence band and an empty conduction band, topological insulators maintain a band gap in the bulk but have protected conducting states on their edges or surfaces. These conducting states are immune to certain types of disorder and defects, making them robust against changes in surface geometry and chemistry. This robustness is attributed to the preservation of time-reversal symmetry and the presence of spin-orbit coupling, which together lead to the formation of topologically protected surface states. The idea of the group, involved into a joint project with Unisalento, IIT, and the ST Microelectronics company, is that to study fundamental physics while simultaneously hypothesizing possible industrial application scenarios for a new class of materials. From a technological standpoint, it is believed that these materials could have various applications ranging from spintronics to quantum information and could contribute to reducing electricity consumption in devices underlying conventional electronics.
People
Stefania D’Agostino, Claudio Corianò
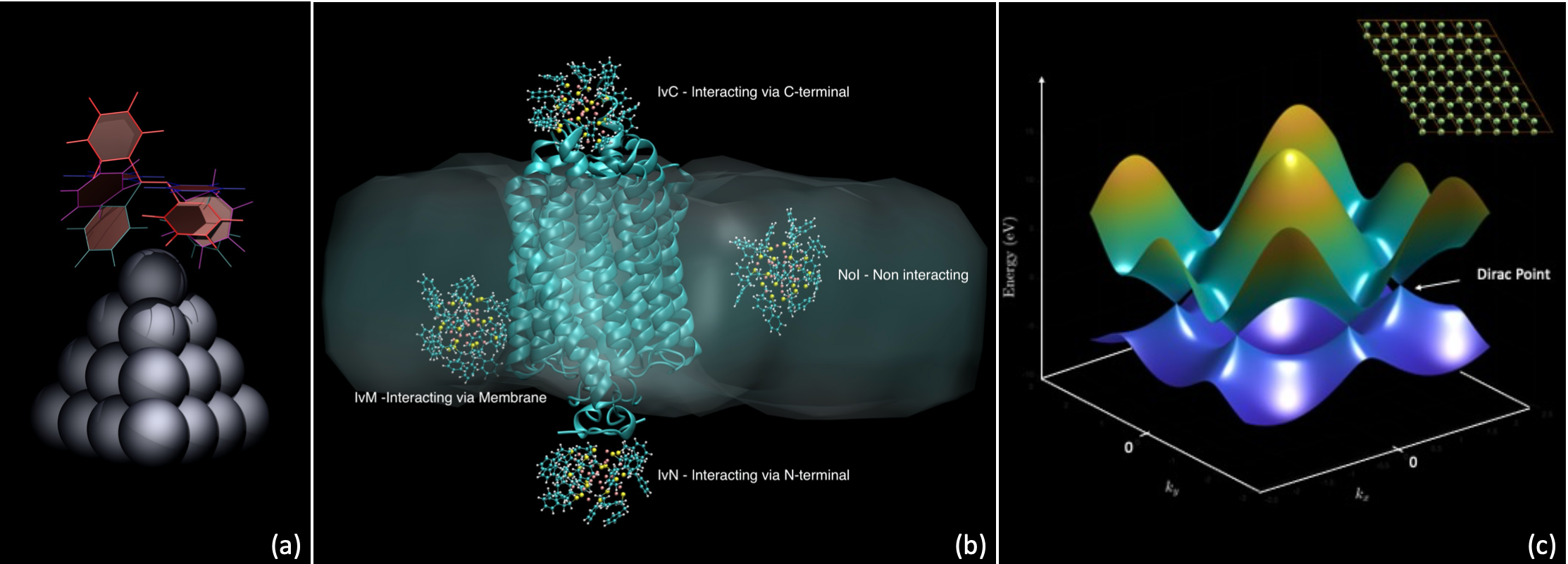
Figure: (a) Ag20 silver cluster interacting with an azobenzene molecule assuming different conformations; (b) Functionalized Au nanocluster interacting with a Channelrhodopsin embedded in a phosphatidylcholine membrane; (c) MATLAB representation of the electronic bands structure of graphene, presenting Dirac cones, features particularly relevant in the study of topological insulators.
Quantitative & statistical image processing
Medical physics is an area of research that develops concepts and methods from physics and applies them to medicine, with main implications in the fields of biomedical imaging and radiation oncology.
Contact Persons
Giuseppe Palma
Keywords
medical physics, image processing, magnetic resonance imaging, radiotherapy, statistical modeling
Its theoretical and computational branches include two research lines related to image analysis and processing: quantitative magnetic resonance imaging (qMRI) and statistical modeling of the radiotherapy (RT) outcomes.
Quantitative Magnetic Resonance Imaging. qMRI differs from traditional MRI by aiming to provide precise measurements of tissue properties, quantifying physical parameters such as relaxation times, diffusion coefficients, and magnetization transfer rates. In particular, the RESUMEN protocol developed by the Nanotec research group represents the state-of-the-art for high-resolution quantification of tissue parameters in times compatible with clinical practice. These quantitative measurements offer valuable insights into tissue composition, microstructure, and function, enabling more accurate diagnosis and monitoring of various pathophysiological conditions. The primary application of qMRI is in neuroimaging, allowing characterization of brain tissue alterations associated with conditions such as multiple sclerosis, neurodegenerative disorders, and brain tumors. Also, qMRI is increasingly used in musculoskeletal imaging to assess cartilage integrity, in cardiac imaging to study myocardial function and viability, and in oncology for tumor characterization and treatment response assessment.
Statistical modeling of radiotherapy outcomes. The use of RT in oncology is based on the analysis of a particularly narrow therapeutic window, which is subject to a multitude of factors that interact in surprisingly complex ways. Modeling the outcomes of RT, both in terms of tumor control and the onset of toxicity, heavily relies on advanced statistical methods to analyze a wide range of factors that influence patient response, including the quality and the dose of radiation delivered, tumor location, biological characteristics of surrounding tissues, and individual patient factors. In particular, the Nanotec research group has developed techniques for the spatial analysis of organ radiosensitivity, developing an open-source software for voxel-based analyses of the relationships between tissue dose distribution and treatment response. Integrating complex statistical models with clinical and radiological data provides a comprehensive overview of the variables influencing the success of RT treatment, enabling oncologists to make informed and personalized decisions for each patient and playing a crucial role in the development of more effective therapeutic protocols and the advancement of oncological research.
People
Tizio Caio Sempronio
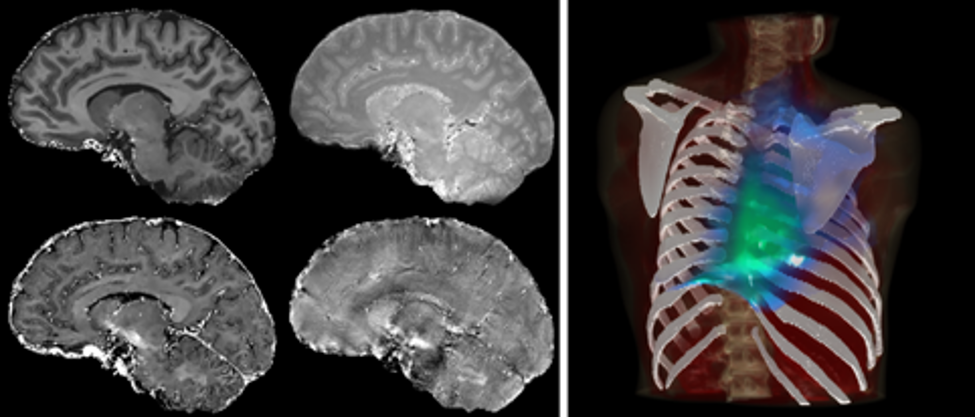
Figure: Left panel: sagittal view of four RESUMEN qMRI parameters of the brain tissues; right panel: 3D rendering of the correlation between RT dose and lymphocyte depletion in lung cancer treatment.
